문제 설명
요약하면, 주어진 삼각형 구조의 꼭대기부터 시작하여, 아래로 내려갈 때 대각선 왼쪽 또는 오른쪽으로만 이동 가능하다는 조건 하에, 경로상의 숫자 합 중 최댓값을 구하는 문제이다.
https://school.programmers.co.kr/learn/courses/30/lessons/43105
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
풀이 과정
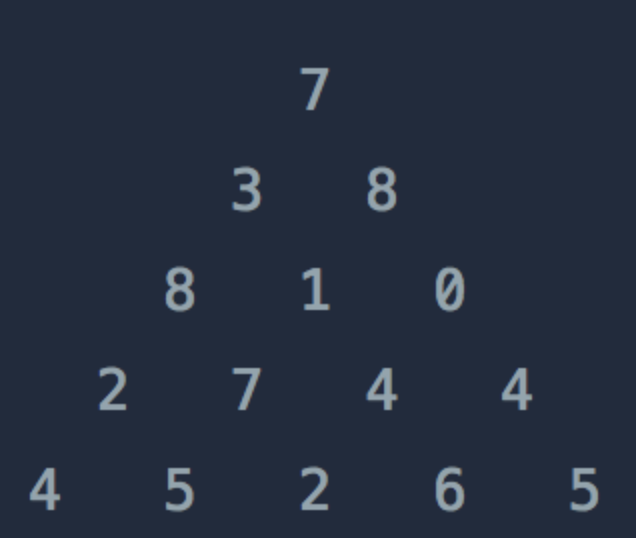
삼각형의 각 칸은 자신의 좌측 상단 혹은 우측 상단들의 값에 영향을 받는다. 따라서, 반복문을 진행하며 삼각형 각 칸의 값을 최댓값으로 업데이트해나가는 DP 로 풀이하였다.
아래와 같이 삼각형의 형태를 직각삼각형 형태로 생각하면 로직을 구현하기 편하다.
[7],
[3, 8],
[8, 1, 0],
[2, 7, 4, 4],
[4, 5, 2, 6, 5]
위 형태에서, 꼭대기에서 바닥으로 가면서 삼각형의 각 칸의 값을 현재 칸까지의 최댓값으로 업데이트할 때,
삼각형의 [i][0] 값은 좌측 상단 값이 없기 때문에 항상 [i-1][0]+[i][0] 이고
삼각형의 [i][i] 값은 우측 상단 값이 없기 때문에 [i-1][i-1]+[i][i] 이다.
코드로 나타내면 아래와 같다.
for(int i=1;i<n;i++){
arr[i][0]+=arr[i-1][0];
arr[i][i]+=arr[i-1][i-1];
}
꼭대기에서 바닥으로 이동할 때 현재 칸을 기준으로 좌측 상단 또는 우측 상단의 값을 비교하여 큰 값을 채택하고 현재 칸의 값과 더하여 현재 칸까지의 값을 결정한다. 코드로 구현하면 아래와 같다.
arr[i][j] += max(arr[i-1][j-1],arr[i-1][j]);
위와 같은 로직으로 삼각형 각 칸의 값을 업데이트 해나가면 가장 바닥 열에는 각 칸까지의 최댓값이 저장된다.
이 값들 중에서 최댓값이 정답이 된다.
#include <string>
#include <cmath>
#include <vector>
#include <iostream>
using namespace std;
int arr[501][501];
int solution(vector<vector<int>> triangle) {
int answer = 0;
int n =triangle.size();
for(int i=0;i<n;i++){
for(int j=0;j<triangle[i].size();j++){
arr[i][j]=triangle[i][j];
}
}
if(n<3){ // 높이 1 또는 2인 경우.
answer = arr[0][0] + max(arr[1][0],arr[1][1]);
}
else{
for(int i=1;i<n;i++){
arr[i][0]+=arr[i-1][0];
arr[i][i]+=arr[i-1][i-1];
}
for(int i=2;i<n;i++){
for(int j=1;j<i;j++){
arr[i][j] += max(arr[i-1][j-1],arr[i-1][j]);
}
}
}
for(int i=0;i<n;i++){
answer = max(answer, arr[n-1][i]);
}
return answer;
}'Algorithm' 카테고리의 다른 글
| [프로그래머스] 베스트앨범 (0) | 2024.11.05 |
|---|---|
| [백준 17616] 등수 찾기 (0) | 2023.06.27 |
| [백준 2539] 모자이크 (0) | 2023.06.20 |
| [백준 2638] 치즈 (1) | 2023.02.17 |
| [백준 2528] 사다리 (0) | 2023.01.13 |
문제 설명
요약하면, 주어진 삼각형 구조의 꼭대기부터 시작하여, 아래로 내려갈 때 대각선 왼쪽 또는 오른쪽으로만 이동 가능하다는 조건 하에, 경로상의 숫자 합 중 최댓값을 구하는 문제이다.
https://school.programmers.co.kr/learn/courses/30/lessons/43105
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
풀이 과정

삼각형의 각 칸은 자신의 좌측 상단 혹은 우측 상단들의 값에 영향을 받는다. 따라서, 반복문을 진행하며 삼각형 각 칸의 값을 최댓값으로 업데이트해나가는 DP 로 풀이하였다.
아래와 같이 삼각형의 형태를 직각삼각형 형태로 생각하면 로직을 구현하기 편하다.
[7],
[3, 8],
[8, 1, 0],
[2, 7, 4, 4],
[4, 5, 2, 6, 5]
위 형태에서, 꼭대기에서 바닥으로 가면서 삼각형의 각 칸의 값을 현재 칸까지의 최댓값으로 업데이트할 때,
삼각형의 [i][0] 값은 좌측 상단 값이 없기 때문에 항상 [i-1][0]+[i][0] 이고
삼각형의 [i][i] 값은 우측 상단 값이 없기 때문에 [i-1][i-1]+[i][i] 이다.
코드로 나타내면 아래와 같다.
for(int i=1;i<n;i++){
arr[i][0]+=arr[i-1][0];
arr[i][i]+=arr[i-1][i-1];
}
꼭대기에서 바닥으로 이동할 때 현재 칸을 기준으로 좌측 상단 또는 우측 상단의 값을 비교하여 큰 값을 채택하고 현재 칸의 값과 더하여 현재 칸까지의 값을 결정한다. 코드로 구현하면 아래와 같다.
arr[i][j] += max(arr[i-1][j-1],arr[i-1][j]);
위와 같은 로직으로 삼각형 각 칸의 값을 업데이트 해나가면 가장 바닥 열에는 각 칸까지의 최댓값이 저장된다.
이 값들 중에서 최댓값이 정답이 된다.
#include <string>
#include <cmath>
#include <vector>
#include <iostream>
using namespace std;
int arr[501][501];
int solution(vector<vector<int>> triangle) {
int answer = 0;
int n =triangle.size();
for(int i=0;i<n;i++){
for(int j=0;j<triangle[i].size();j++){
arr[i][j]=triangle[i][j];
}
}
if(n<3){ // 높이 1 또는 2인 경우.
answer = arr[0][0] + max(arr[1][0],arr[1][1]);
}
else{
for(int i=1;i<n;i++){
arr[i][0]+=arr[i-1][0];
arr[i][i]+=arr[i-1][i-1];
}
for(int i=2;i<n;i++){
for(int j=1;j<i;j++){
arr[i][j] += max(arr[i-1][j-1],arr[i-1][j]);
}
}
}
for(int i=0;i<n;i++){
answer = max(answer, arr[n-1][i]);
}
return answer;
}'Algorithm' 카테고리의 다른 글
| [프로그래머스] 베스트앨범 (0) | 2024.11.05 |
|---|---|
| [백준 17616] 등수 찾기 (0) | 2023.06.27 |
| [백준 2539] 모자이크 (0) | 2023.06.20 |
| [백준 2638] 치즈 (1) | 2023.02.17 |
| [백준 2528] 사다리 (0) | 2023.01.13 |
